Perfect Binary Tree
In this tutorial, you will learn about the perfect binary tree. Also, you will find working examples for checking a perfect binary tree in C, C++, Java and Python.
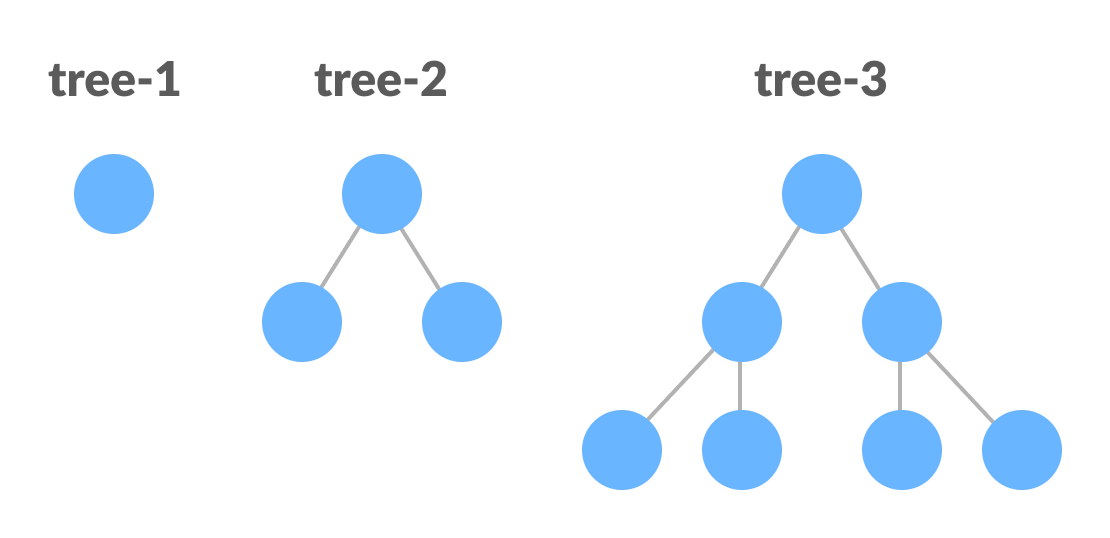
A perfect binary tree is a type of binary tree in which every internal node has exactly two child nodes and all the leaf nodes are at the same level.

All the internal nodes have a degree of 2.
Recursively, a perfect binary tree can be defined as:
- If a single node has no children, it is a perfect binary tree of height
h = 0, - If a node has
h > 0, it is a perfect binary tree if both of its subtrees are of heighth - 1and are non-overlapping.
Python Examples
The following code is for checking whether a tree is a perfect binary tree.
/* Checking if a binary tree is a perfect binary tree in Python */
class newNode:
def __init__(self, k):
self.key = k
self.right = self.left = None
/* Calculate the depth */
def calculateDepth(node):
d = 0
while (node is not None):
d += 1
node = node.left
return d
/* Check if the tree is perfect binary tree */
def is_perfect(root, d, level=0):
/* Check if the tree is empty */
if (root is None):
return True
/* Check the presence of trees */
if (root.left is None and root.right is None):
return (d == level + 1)
if (root.left is None or root.right is None):
return False
return (is_perfect(root.left, d, level + 1) and
is_perfect(root.right, d, level + 1))
root = None
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)
if (is_perfect(root, calculateDepth(root))):
print("The tree is a perfect binary tree")
else:
print("The tree is not a perfect binary tree")Perfect Binary Tree Theorems
- A perfect binary tree of height h has
2h + 1 – 1node. - A perfect binary tree with n nodes has height
log(n + 1) – 1 = Θ(ln(n)). - A perfect binary tree of height h has
2hleaf nodes. - The average depth of a node in a perfect binary tree is
Θ(ln(n)).
Python Example for Beginners
Two Machine Learning Fields
There are two sides to machine learning:
- Practical Machine Learning:This is about querying databases, cleaning data, writing scripts to transform data and gluing algorithm and libraries together and writing custom code to squeeze reliable answers from data to satisfy difficult and ill defined questions. It’s the mess of reality.
- Theoretical Machine Learning: This is about math and abstraction and idealized scenarios and limits and beauty and informing what is possible. It is a whole lot neater and cleaner and removed from the mess of reality.
Data Science Resources: Data Science Recipes and Applied Machine Learning Recipes
Introduction to Applied Machine Learning & Data Science for Beginners, Business Analysts, Students, Researchers and Freelancers with Python & R Codes @ Western Australian Center for Applied Machine Learning & Data Science (WACAMLDS) !!!
Latest end-to-end Learn by Coding Recipes in Project-Based Learning:
Applied Statistics with R for Beginners and Business Professionals
Data Science and Machine Learning Projects in Python: Tabular Data Analytics
Data Science and Machine Learning Projects in R: Tabular Data Analytics
Python Machine Learning & Data Science Recipes: Learn by Coding
R Machine Learning & Data Science Recipes: Learn by Coding
Comparing Different Machine Learning Algorithms in Python for Classification (FREE)
Disclaimer: The information and code presented within this recipe/tutorial is only for educational and coaching purposes for beginners and developers. Anyone can practice and apply the recipe/tutorial presented here, but the reader is taking full responsibility for his/her actions. The author (content curator) of this recipe (code / program) has made every effort to ensure the accuracy of the information was correct at time of publication. The author (content curator) does not assume and hereby disclaims any liability to any party for any loss, damage, or disruption caused by errors or omissions, whether such errors or omissions result from accident, negligence, or any other cause. The information presented here could also be found in public knowledge domains.
