Python Python Algorithms Python Data Structure

Python Data Structure and Algorithm Tutorial – AVL Tree

By on Thursday, June 10, 2021

AVL Tree

 

In this tutorial, you will learn what an avl tree is. Also, you will find working examples of various operations performed on an avl tree in C, C++, Java and Python.

AVL tree is a self-balancing binary search tree in which each node maintains extra information called a balance factor whose value is either -1, 0 or +1.

AVL tree got its name after its inventor Georgy Adelson-Velsky and Landis.

Balance Factor

Balance factor of a node in an AVL tree is the difference between the height of the left subtree and that of the right subtree of that node.

Balance Factor = (Height of Left Subtree – Height of Right Subtree) or (Height of Right Subtree – Height of Left Subtree)

The self balancing property of an avl tree is maintained by the balance factor. The value of balance factor should always be -1, 0 or +1.

An example of a balanced avl tree is:

avl tree
Avl tree

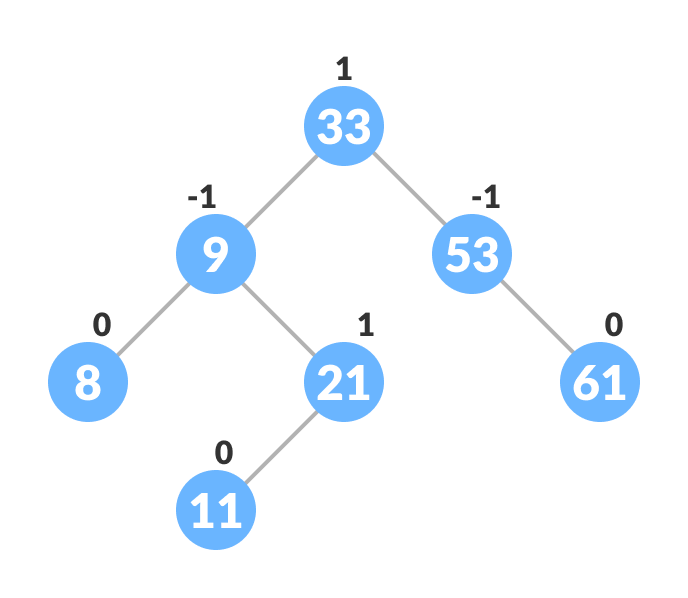
Operations on an AVL tree

Various operations that can be performed on an AVL tree are:

Rotating the subtrees in an AVL Tree

In rotation operation, the positions of the nodes of a subtree are interchanged.

There are two types of rotations:

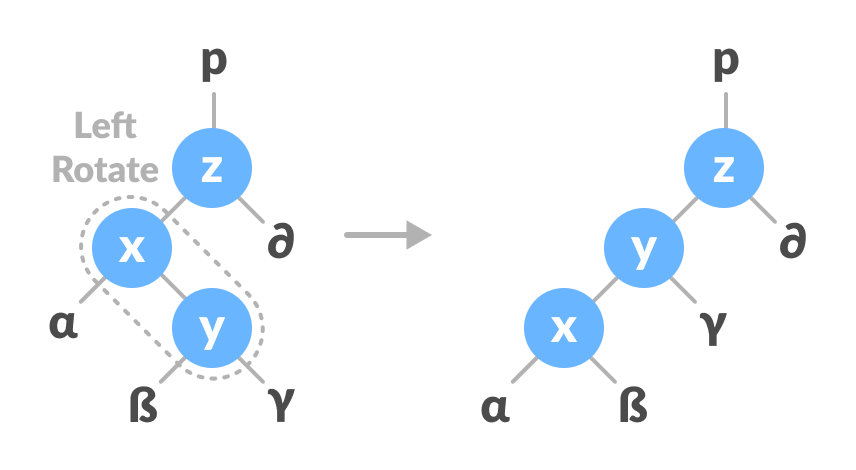
Left Rotate

In left-rotation, the arrangement of the nodes on the right is transformed into the arrangements on the left node.

Algorithm

  1. Let the initial tree be:
    left-rotate
    Left rotate
  2. If y has a left subtree, assign x as the parent of the left subtree of y.
    left-rotate
    Assign x as the parent of the left subtree of y
  3. If the parent of x is NULL, make y as the root of the tree.
  4. Else if x is the left child of p, make y as the left child of p.
  5. Else assign y as the right child of p.
    left-rotate
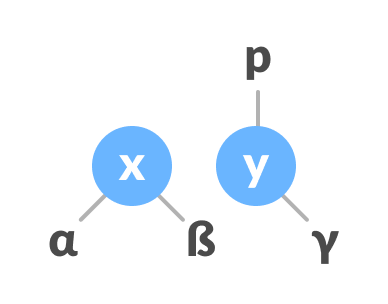
    Change the parent of x to that of y
  6. Make y as the parent of x.
    left-rotate
    Assign y as the parent of x.

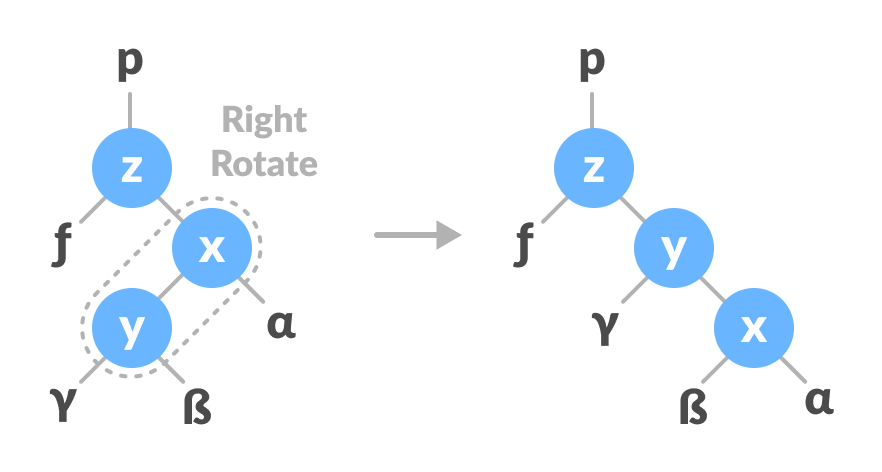
Right Rotate

In left-rotation, the arrangement of the nodes on the left is transformed into the arrangements on the right node.

  1. Let the initial tree be:
    right-rotate
    Initial tree
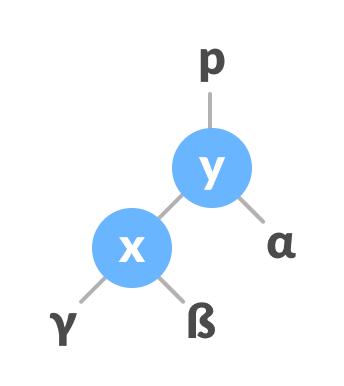
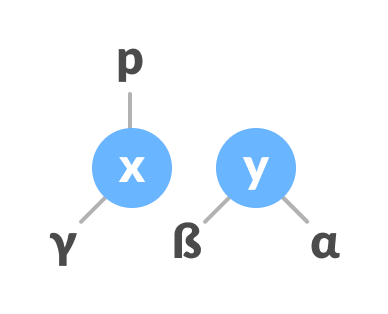
  2. If x has a right subtree, assign y as the parent of the right subtree of x.
    right-rotate
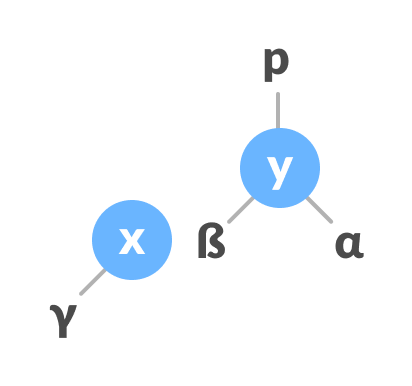
    Assign y as the parent of the right subtree of x
  3. If the parent of y is NULL, make x as the root of the tree.
  4. Else if y is the right child of its parent p, make x as the right child of p.
  5. Else assign x as the left child of p.
    right-rotate
    Assign the parent of y as the parent of x.
  6. Make x as the parent of y.
    right-rotate
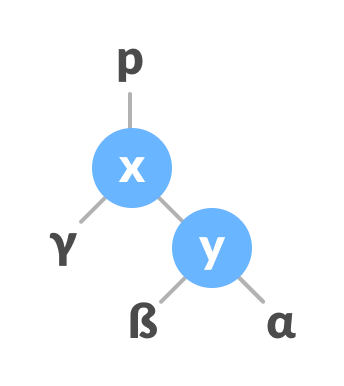
    Assign x as the parent of y

Left-Right and Right-Left Rotate

In left-right rotation, the arrangements are first shifted to the left and then to the right.

  1. Do left rotation on x-y.
    left-right rotate
    Left rotate x-y
  2. Do right rotation on y-z.
    left-right rotate
    Right rotate z-y

In right-left rotation, the arrangements are first shifted to the right and then to the left.

  1. Do right rotation on x-y.
    right-left rotate
    Right rotate x-y
  2. Do left rotation on z-y.
    right-left rotate
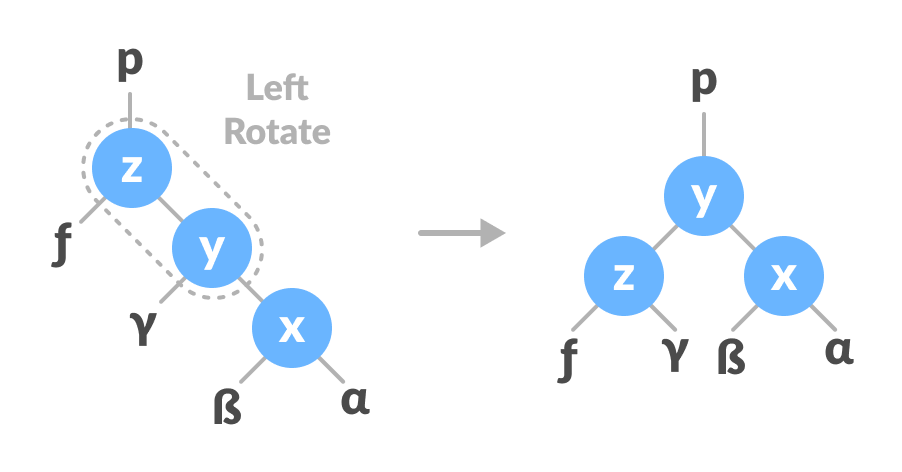
    Left rotate z-y

Algorithm to insert a newNode

A newNode is always inserted as a leaf node with balance factor equal to 0.

  1. Let the initial tree be:
    initial tree
    Initial tree for insertion

    Let the node to be inserted be:

    new node
    New node
  2. Go to the appropriate leaf node to insert a newNode using the following recursive steps. Compare newKey with rootKey of the current tree.
    1. If newKey < rootKey, call insertion algorithm on the left subtree of the current node until the leaf node is reached.
    2. Else if newKey > rootKey, call insertion algorithm on the right subtree of current node until the leaf node is reached.
    3. Else, return leafNode.
      avl tree insertion
      Finding the location to insert newNode
  3. Compare leafKey obtained from the above steps with newKey:
    1. If newKey < leafKey, make newNode as the leftChild of leafNode.
    2. Else, make newNode as rightChild of leafNode.
      avl tree insertion
      Inserting the new node
  4. Update balanceFactor of the nodes.
    avl tree insertion
    Updating the balance factor after insertion
  5. If the nodes are unbalanced, then rebalance the node.
    1. If balanceFactor > 1, it means the height of the left subtree is greater than that of the right subtree. So, do a right rotation or left-right rotation
      1. If newNodeKey < leftChildKey do right rotation.
      2. Else, do left-right rotation.
        insertion in avl tree
        Balancing the tree with rotation
        insertion in avl tree
        Balancing the tree with rotation
    2. If balanceFactor < -1, it means the height of the right subtree is greater than that of the left subtree. So, do right rotation or right-left rotation
      1. If newNodeKey > rightChildKey do left rotation.
      2. Else, do right-left rotation
  6. The final tree is:
    left-right insertion
    Final balanced tree

Algorithm to Delete a node

A node is always deleted as a leaf node. After deleting a node, the balance factors of the nodes get changed. In order to rebalance the balance factor, suitable rotations are performed.

  1. Locate nodeToBeDeleted (recursion is used to find nodeToBeDeleted in the code used below).
    node to be deleted
    Locating the node to be deleted
  2. There are three cases for deleting a node:
    1. If nodeToBeDeleted is the leaf node (ie. does not have any child), then remove nodeToBeDeleted.
    2. If nodeToBeDeleted has one child, then substitute the contents of nodeToBeDeleted with that of the child. Remove the child.
    3. If nodeToBeDeleted has two children, find the inorder successor w of nodeToBeDeleted (ie. node with a minimum value of key in the right subtree).
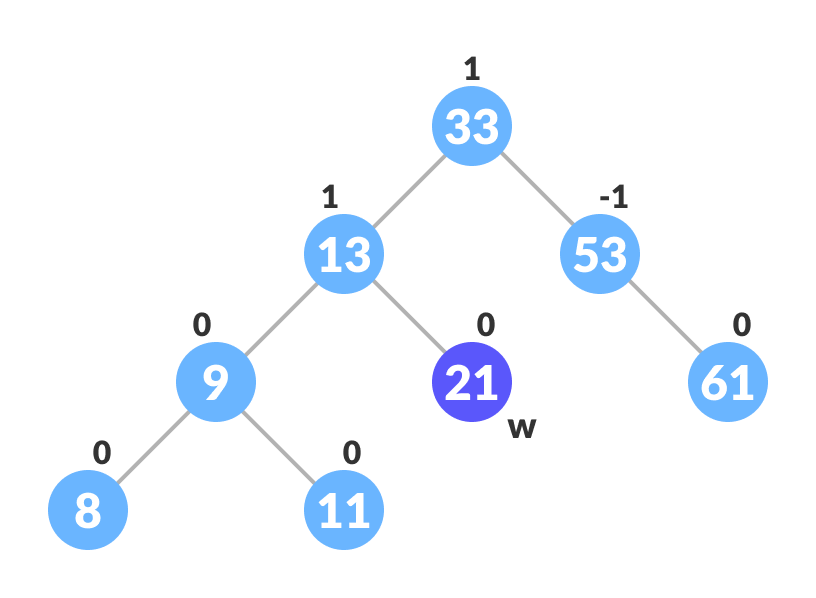
      finding the successor
      Finding the successor
      1. Substitute the contents of nodeToBeDeleted with that of w.
        substitute the node to be deleted
        Substitute the node to be deleted
      2. Remove the leaf node w.
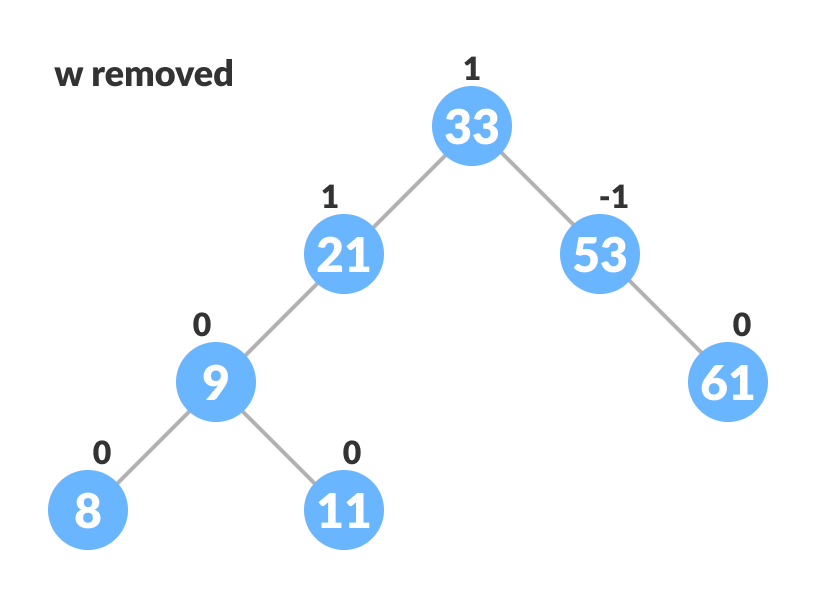
        remove w
        Remove w
  3. Update balanceFactor of the nodes.
    update bf
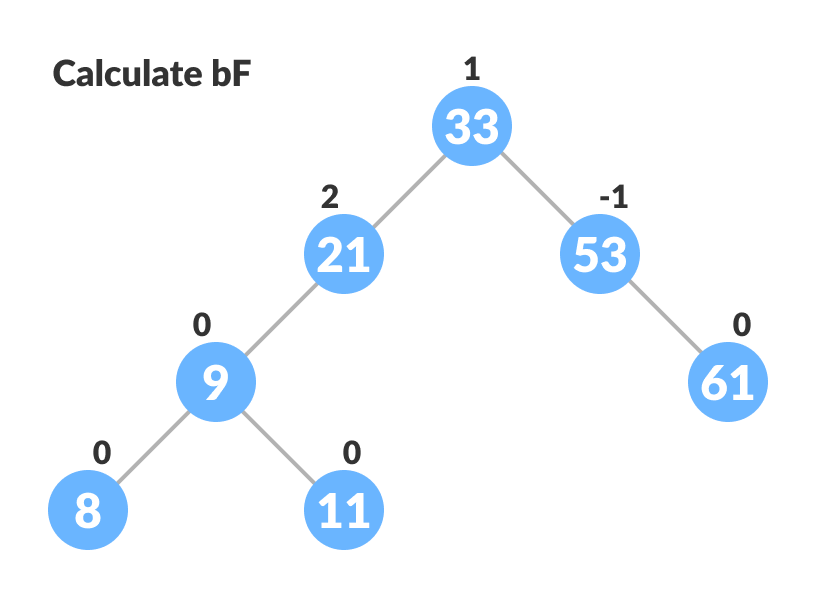
    Update bf
  4. Rebalance the tree if the balance factor of any of the nodes is not equal to -1, 0 or 1.
    1. If balanceFactor of currentNode > 1,
      1. If balanceFactor of leftChild >= 0, do right rotation.
        right-rotate
        Right-rotate for balancing the tree
      2. Else do left-right rotation.
    2. If balanceFactor of currentNode < -1,
      1. If balanceFactor of rightChild <= 0, do left rotation.
      2. Else do right-left rotation.
  5. The final tree is:
    avl tree
    Avl tree final

Python, Java and C/C++ Examples

/* AVL tree implementation in Python */


import sys

/* Create a tree node */
class TreeNode(object):
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.height = 1


class AVLTree(object):

    /* Function to insert a node */
    def insert_node(self, root, key):

        /* Find the correct location and insert the node */
        if not root:
            return TreeNode(key)
        elif key < root.key:
            root.left = self.insert_node(root.left, key)
        else:
            root.right = self.insert_node(root.right, key)

        root.height = 1 + max(self.getHeight(root.left),
                              self.getHeight(root.right))

        /* Update the balance factor and balance the tree */
        balanceFactor = self.getBalance(root)
        if balanceFactor > 1:
            if key < root.left.key:
                return self.rightRotate(root)
            else:
                root.left = self.leftRotate(root.left)
                return self.rightRotate(root)

        if balanceFactor < -1:
            if key > root.right.key:
                return self.leftRotate(root)
            else:
                root.right = self.rightRotate(root.right)
                return self.leftRotate(root)

        return root

    /* Function to delete a node */
    def delete_node(self, root, key):

        /* Find the node to be deleted and remove it */
        if not root:
            return root
        elif key < root.key:
            root.left = self.delete_node(root.left, key)
        elif key > root.key:
            root.right = self.delete_node(root.right, key)
        else:
            if root.left is None:
                temp = root.right
                root = None
                return temp
            elif root.right is None:
                temp = root.left
                root = None
                return temp
            temp = self.getMinValueNode(root.right)
            root.key = temp.key
            root.right = self.delete_node(root.right,
                                          temp.key)
        if root is None:
            return root

        /* Update the balance factor of nodes */
        root.height = 1 + max(self.getHeight(root.left),
                              self.getHeight(root.right))

        balanceFactor = self.getBalance(root)

        /* Balance the tree */
        if balanceFactor > 1:
            if self.getBalance(root.left) >= 0:
                return self.rightRotate(root)
            else:
                root.left = self.leftRotate(root.left)
                return self.rightRotate(root)
        if balanceFactor < -1:
            if self.getBalance(root.right) <= 0:
                return self.leftRotate(root)
            else:
                root.right = self.rightRotate(root.right)
                return self.leftRotate(root)
        return root

    /* Function to perform left rotation */
    def leftRotate(self, z):
        y = z.right
        T2 = y.left
        y.left = z
        z.right = T2
        z.height = 1 + max(self.getHeight(z.left),
                           self.getHeight(z.right))
        y.height = 1 + max(self.getHeight(y.left),
                           self.getHeight(y.right))
        return y

    /* Function to perform right rotation */
    def rightRotate(self, z):
        y = z.left
        T3 = y.right
        y.right = z
        z.left = T3
        z.height = 1 + max(self.getHeight(z.left),
                           self.getHeight(z.right))
        y.height = 1 + max(self.getHeight(y.left),
                           self.getHeight(y.right))
        return y

    /* Get the height of the node */
    def getHeight(self, root):
        if not root:
            return 0
        return root.height

    /* Get balance factore of the node */
    def getBalance(self, root):
        if not root:
            return 0
        return self.getHeight(root.left) - self.getHeight(root.right)

    def getMinValueNode(self, root):
        if root is None or root.left is None:
            return root
        return self.getMinValueNode(root.left)

    def preOrder(self, root):
        if not root:
            return
        print("{0} ".format(root.key), end="")
        self.preOrder(root.left)
        self.preOrder(root.right)

    /* Print the tree */
    def printHelper(self, currPtr, indent, last):
        if currPtr != None:
            sys.stdout.write(indent)
            if last:
                sys.stdout.write("R----")
                indent += "     "
            else:
                sys.stdout.write("L----")
                indent += "|    "
            print(currPtr.key)
            self.printHelper(currPtr.left, indent, False)
            self.printHelper(currPtr.right, indent, True)


myTree = AVLTree()
root = None
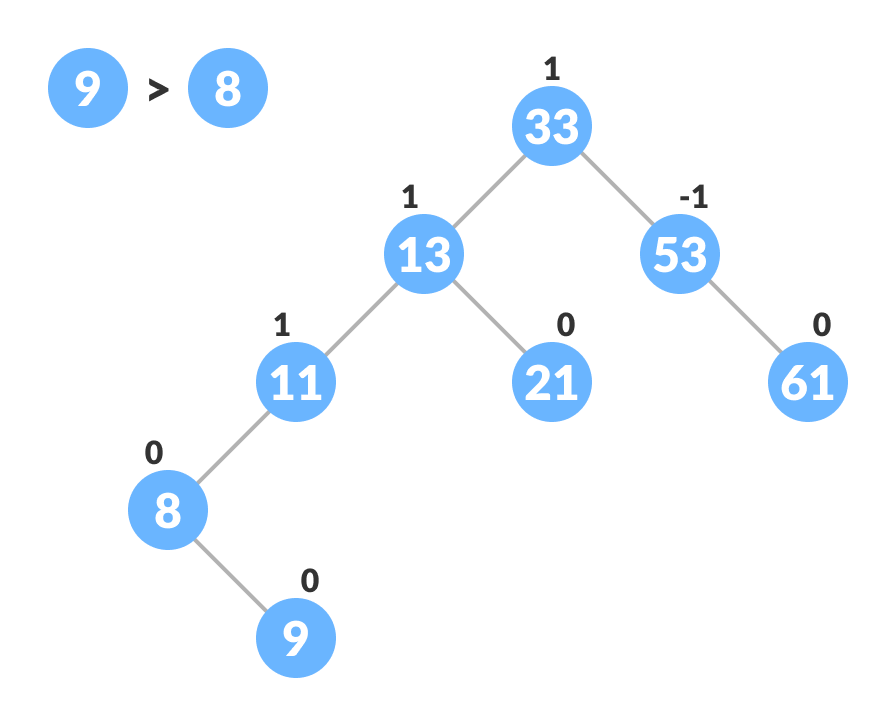
nums = [33, 13, 52, 9, 21, 61, 8, 11]
for num in nums:
    root = myTree.insert_node(root, num)
myTree.printHelper(root, "", True)
key = 13
root = myTree.delete_node(root, key)
print("After Deletion: ")
myTree.printHelper(root, "", True)

Complexities of Different Operations on an AVL Tree

Insertion Deletion Search
O(log n) O(log n) O(log n)

AVL Tree Applications

  • For indexing large records in databases
  • For searching in large databases

 

 

Python Example for Beginners

Two Machine Learning Fields

There are two sides to machine learning:

  • Practical Machine Learning:This is about querying databases, cleaning data, writing scripts to transform data and gluing algorithm and libraries together and writing custom code to squeeze reliable answers from data to satisfy difficult and ill defined questions. It’s the mess of reality.
  • Theoretical Machine Learning: This is about math and abstraction and idealized scenarios and limits and beauty and informing what is possible. It is a whole lot neater and cleaner and removed from the mess of reality.

 

Data Science Resources: Data Science Recipes and Applied Machine Learning Recipes

Introduction to Applied Machine Learning & Data Science for Beginners, Business Analysts, Students, Researchers and Freelancers with Python & R Codes @ Western Australian Center for Applied Machine Learning & Data Science (WACAMLDS) !!!

Latest end-to-end Learn by Coding Recipes in Project-Based Learning:

Applied Statistics with R for Beginners and Business Professionals

Data Science and Machine Learning Projects in Python: Tabular Data Analytics

Data Science and Machine Learning Projects in R: Tabular Data Analytics

Python Machine Learning & Data Science Recipes: Learn by Coding

R Machine Learning & Data Science Recipes: Learn by Coding

Comparing Different Machine Learning Algorithms in Python for Classification (FREE)

Disclaimer: The information and code presented within this recipe/tutorial is only for educational and coaching purposes for beginners and developers. Anyone can practice and apply the recipe/tutorial presented here, but the reader is taking full responsibility for his/her actions. The author (content curator) of this recipe (code / program) has made every effort to ensure the accuracy of the information was correct at time of publication. The author (content curator) does not assume and hereby disclaims any liability to any party for any loss, damage, or disruption caused by errors or omissions, whether such errors or omissions result from accident, negligence, or any other cause. The information presented here could also be found in public knowledge domains.

Google –> SETScholars

0
Related Posts