Write a Python program to calculate magic square.

A magic square is an arrangement of distinct numbers (i.e., each number is used once), usually integers, in a square grid, where the numbers in each row, and in each column, and the numbers in the main and secondary diagonals, all add up to the same number, called the “magic constant.” A magic square has the same number of rows as it has columns, and in conventional math notation, “n” stands for the number of rows (and columns) it has. Thus, a magic square always contains n2 numbers, and its size (the number of rows [and columns] it has) is described as being “of order n”.

Pictorial presentation:

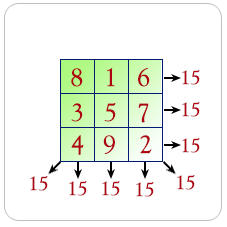
Sample Solution:

Python Code:

def magic_square_test(my_matrix):
    iSize = len(my_matrix[0])
    sum_list = []
    
    Horizontal Part:
    sum_list.extend([sum (lines) for lines in my_matrix])   

    Vertical Part:
    for col in range(iSize):
        sum_list.append(sum(row[col] for row in my_matrix))
    
    Diagonals Part
    result1 = 0
    for i in range(0,iSize):
        result1 +=my_matrix[i][i]
    sum_list.append(result1)  
    
    result2 = 0
    for i in range(iSize-1,-1,-1):
        result2 +=my_matrix[i][i]
    sum_list.append(result2)

    if len(set(sum_list))>1:
        return False
    return True

m=[[7, 12, 1, 14], [2, 13, 8, 11], [16, 3, 10, 5], [9, 6, 15, 4]] 
print(magic_square_test(m));

m=[[2, 7, 6], [9, 5, 1], [4, 3, 8]]
print(magic_square_test(m));

m=[[2, 7, 6], [9, 5, 1], [4, 3, 7]]
print(magic_square_test(m));

Sample Output:

True                                                                                                          
True                                                                                                          
False

Write a Python program to calculate magic square

Disclaimer: The information and code presented within this recipe/tutorial is only for educational and coaching purposes for beginners and developers. Anyone can practice and apply the recipe/tutorial presented here, but the reader is taking full responsibility for his/her actions. The author (content curator) of this recipe (code / program) has made every effort to ensure the accuracy of the information was correct at time of publication. The author (content curator) does not assume and hereby disclaims any liability to any party for any loss, damage, or disruption caused by errors or omissions, whether such errors or omissions result from accident, negligence, or any other cause. The information presented here could also be found in public knowledge domains.