
(Python Example for Beginners)
Write a NumPy program to calculate the QR decomposition of a given matrix.
From Wikipedia: In linear algebra, a QR decomposition (also called a QR factorization) of a matrix is a decomposition of a matrix A into a product A = QR of an orthogonal matrix Q and an upper triangular matrix R. QR decomposition is often used to solve the linear least squares problem and is the basis for a particular eigenvalue algorithm, the QR algorithm.
Square matrix
Any real square matrix A may be decomposed as
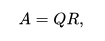
where Q is an orthogonal matrix (its columns are orthogonal unit vectors meaning {displaystyle Q^{textsf {T}}Q=QQ^{textsf {T}}=I} {displaystyle Q^{textsf {T}}Q=QQ^{textsf {T}}=I}) and R is an upper triangular matrix (also called right triangular matrix). If A is invertible, then the factorization is unique if we require the diagonal elements of R to be positive.
If instead A is a complex square matrix, then there is a decomposition A = QR where Q is a unitary matrix (so {displaystyle Q^{*}Q=QQ^{*}=I} {displaystyle Q^{*}Q=QQ^{*}=I}).
If A has n linearly independent columns, then the first n columns of Q form an orthonormal basis for the column space of A. More generally, the first k columns of Q form an orthonormal basis for the span of the first k columns of A for any 1 ≤ k ≤ n.[1] The fact that any column k of A only depends on the first k columns of Q is responsible for the triangular form of R.[1]
Sample Solution :
Python Code :
Sample Output:
Original matrix:
[[1 2]
[3 4]]
Decomposition of the said matrix:
(array([[-0.31622777, -0.9486833 ],
[-0.9486833 , 0.31622777]]), array([[-3.16227766, -4.42718872],
[ 0. , -0.63245553]]))
Python Example – Write a NumPy program to evaluate Einstein’s summation convention of two given multidimensional arrays
Two Machine Learning Fields
There are two sides to machine learning:
- Practical Machine Learning:This is about querying databases, cleaning data, writing scripts to transform data and gluing algorithm and libraries together and writing custom code to squeeze reliable answers from data to satisfy difficult and ill defined questions. It’s the mess of reality.
- Theoretical Machine Learning: This is about math and abstraction and idealized scenarios and limits and beauty and informing what is possible. It is a whole lot neater and cleaner and removed from the mess of reality.
Disclaimer: The information and code presented within this recipe/tutorial is only for educational and coaching purposes for beginners and developers. Anyone can practice and apply the recipe/tutorial presented here, but the reader is taking full responsibility for his/her actions. The author (content curator) of this recipe (code / program) has made every effort to ensure the accuracy of the information was correct at time of publication. The author (content curator) does not assume and hereby disclaims any liability to any party for any loss, damage, or disruption caused by errors or omissions, whether such errors or omissions result from accident, negligence, or any other cause. The information presented here could also be found in public knowledge domains.
