A strongly connected component is the portion of a directed graph in which there is a path from each vertex to another vertex. It is applicable only on a directed graph.

For example:

Let us take the graph below.

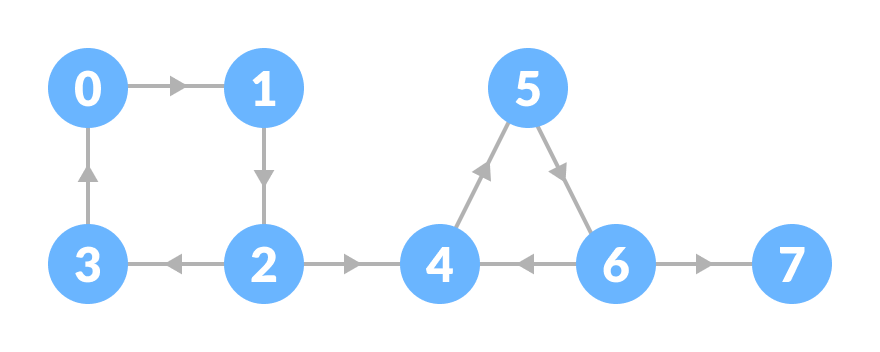
The strongly connected components of the above graph are:

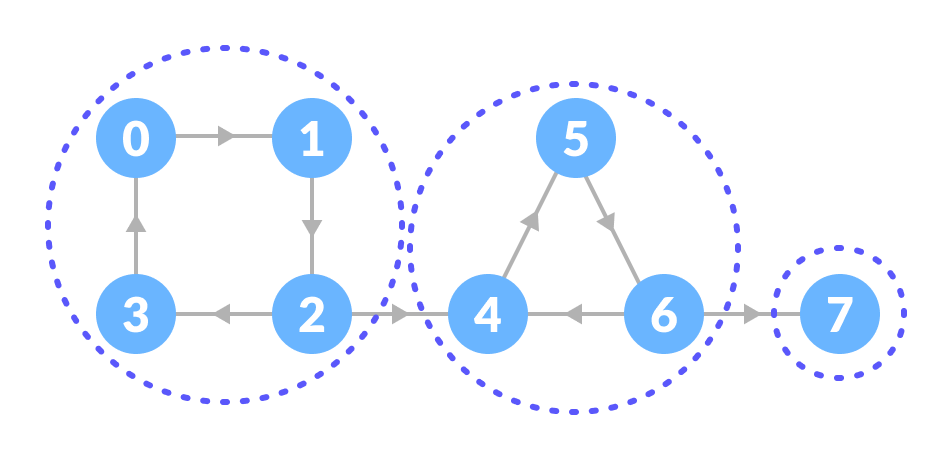
You can observe that in the first strongly connected component, every vertex can reach the other vertex through the directed path.

These components can be found using Kosaraju’s Algorithm.

Kosaraju’s Algorithm

Kosaraju’s Algorithm is based on the depth-first search algorithm implemented twice.

Three steps are involved.

1. Perform a depth first search on the whole graph.Let us start from vertex-0, visit all of its child vertices, and mark the visited vertices as done. If a vertex leads to an already visited vertex, then push this vertex to the stack.

   For example: Starting from vertex-0, go to vertex-1, vertex-2, and then to vertex-3. Vertex-3 leads to already visited vertex-0, so push the source vertex (ie. vertex-3) into the stack.

   

   Go to the previous vertex (vertex-2) and visit its child vertices i.e. vertex-4, vertex-5, vertex-6 and vertex-7 sequentially. Since there is nowhere to go from vertex-7, push it into the stack.

   

   Go to the previous vertex (vertex-6) and visit its child vertices. But, all of its child vertices are visited, so push it into the stack.

   

   Similarly, a final stack is created.

   

2. Reverse the original graph.
   

   

3. Perform depth-first search on the reversed graph.Start from the top vertex of the stack. Traverse through all of its child vertices. Once the already visited vertex is reached, one strongly connected component is formed.

   For example: Pop vertex-0 from the stack. Starting from vertex-0, traverse through its child vertices (vertex-0, vertex-1, vertex-2, vertex-3 in sequence) and mark them as visited. The child of vertex-3 is already visited, so these visited vertices form one strongly connected component.

   

   Go to the stack and pop the top vertex if already visited. Otherwise, choose the top vertex from the stack and traverse through its child vertices as presented above.

   

   

4. Thus, the strongly connected components are:
   

   

Python Examples

/* Kosaraju's algorithm to find strongly connected components in Python */

from collections import defaultdict

class Graph:

    def __init__(self, vertex):
        self.V = vertex
        self.graph = defaultdict(list)

    /* Add edge into the graph */
    def add_edge(self, s, d):
        self.graph[s].append(d)

    /* dfs */
    def dfs(self, d, visited_vertex):
        visited_vertex[d] = True
        print(d, end='')
        for i in self.graph[d]:
            if not visited_vertex[i]:
                self.dfs(i, visited_vertex)

    def fill_order(self, d, visited_vertex, stack):
        visited_vertex[d] = True
        for i in self.graph[d]:
            if not visited_vertex[i]:
                self.fill_order(i, visited_vertex, stack)
        stack = stack.append(d)

    /* transpose the matrix */
    def transpose(self):
        g = Graph(self.V)

        for i in self.graph:
            for j in self.graph[i]:
                g.add_edge(j, i)
        return g

    /* Print stongly connected components */
    def print_scc(self):
        stack = []
        visited_vertex = [False] * (self.V)

        for i in range(self.V):
            if not visited_vertex[i]:
                self.fill_order(i, visited_vertex, stack)

        gr = self.transpose()

        visited_vertex = [False] * (self.V)

        while stack:
            i = stack.pop()
            if not visited_vertex[i]:
                gr.dfs(i, visited_vertex)
                print("")


g = Graph(8)
g.add_edge(0, 1)
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(2, 4)
g.add_edge(3, 0)
g.add_edge(4, 5)
g.add_edge(5, 6)
g.add_edge(6, 4)
g.add_edge(6, 7)

print("Strongly Connected Components:")
g.print_scc()

Kosaraju’s Algorithm Complexity

Kosaraju’s algorithm runs in linear time i.e. O(V+E).

Strongly Connected Components Applications

• Vehicle routing applications
• Maps
• Model-checking in formal verification