Divide and Conquer Algorithm
In this tutorial, you will learn how the divide and conquer algorithm works. Also, you will find the comparison between divide and conquer approach and other approach to solve a recursive problem.
A divide and conquer algorithm is a strategy of solving a large problem by
- breaking the problem into smaller sub-problems
- solving the sub-problems, and
- combining them to get the desired output.
How Divide and Conquer Algorithms Work?
Here are the steps involved:
- Divide : Divide the given problem into sub-problems using recursion.
- Conquer: Solve the smaller sub-problems recursively. If the sub-problem is small enough, then solve it directly.
- Combine: Combine the solutions of the sub-problems which is part of the recursive process to get the solution to the actual problem.
Let us understand this concept with the help of an example.
Here, we are going to sort an array using the divide and conquer approach (ie. merge sort).
- Let the given array be:

Array for merge sort - Divide the array into two halves.

Divide the array into two subparts Again, divide each subpart recursively into two halves until you get individual elements.
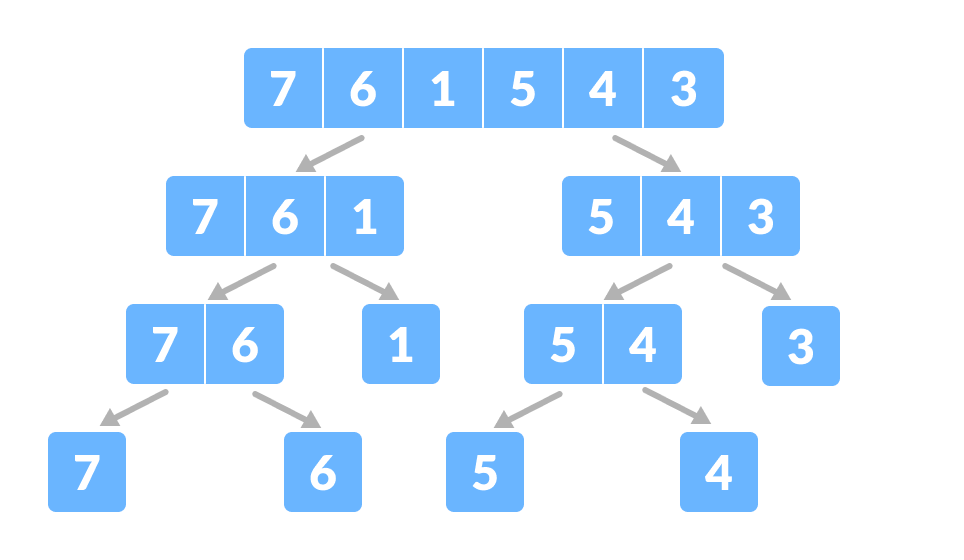
Divide the array into smaller subparts - Now, combine the individual elements in a sorted manner. Here, conquer and combine steps go side by side.
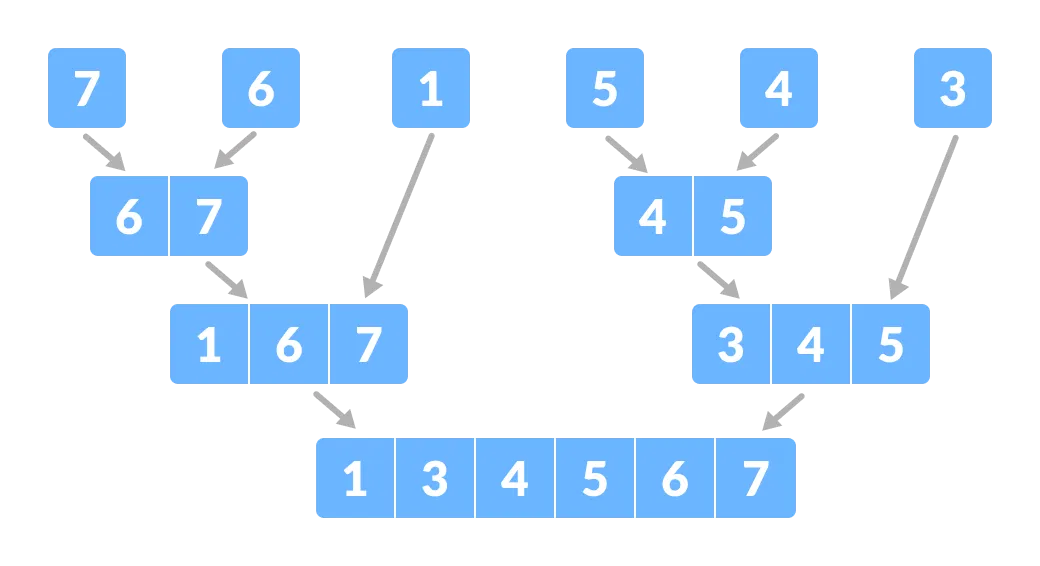
Combine the subparts
Complexity
The complexity of the divide and conquer algorithm is calculated using the master theorem.
T(n) = aT(n/b) + f(n), where, n = size of input a = number of subproblems in the recursion n/b = size of each subproblem. All subproblems are assumed to have the same size. f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
Let us take an example to find the time complexity of a recursive problem.
For a merge sort, the equation can be written as:
T(n) = aT(n/b) + f(n)
= 2T(n/2) + O(n)
Where,
a = 2 (each time, a problem is divided into 2 subproblems)
n/b = n/2 (size of each sub problem is half of the input)
f(n) = time taken to divide the problem and merging the subproblems
T(n/2) = O(n log n) (To understand this, please refer to the master theorem.)
Now, T(n) = 2T(n log n) + O(n)
≈ O(n log n)
Divide and Conquer vs Dynamic approach
The divide and conquer approach divides a problem into smaller subproblems, these subproblems are further solved recursively. The result of each subproblem is not stored for future reference, whereas, in a dynamic approach, the result of each subproblem is stored for future reference.
Use the divide and conquer approach when the same subproblem is not solved multiple times. Use the dynamic approach when the result of a subproblem is to be used multiple times in the future.
Let us understand this with an example. Suppose we are trying to find the Fibonacci series. Then,
Divide and Conquer approach:
fib(n)
If n < 2, return 1
Else , return f(n - 1) + f(n -2)
Dynamic approach:
mem = [ ]
fib(n)
If n in mem: return mem[n]
else,
If n < 2, f = 1
else , f = f(n - 1) + f(n -2)
mem[n] = f
return f
In a dynamic approach, mem stores the result of each subproblem.
Advantage of Divide and Conquer Algorithm
- The complexity for the multiplication of two matrices using the naive method is O(n3), whereas using the divide and conquer approach (ie. Strassen’s matrix multiplication) is O(n2.8074). Other problems such as the Tower of Hanoi are also simplified by this approach.
- This approach is suitable for multiprocessing systems.
- It makes efficient use of memory caches.
Divide and Conquer Application
- Binary Search
- Merge Sort
- Quick Sort
- Strassen’s Matrix multiplication
- Karatsuba Algorithm
Python Example for Beginners
Two Machine Learning Fields
There are two sides to machine learning:
- Practical Machine Learning:This is about querying databases, cleaning data, writing scripts to transform data and gluing algorithm and libraries together and writing custom code to squeeze reliable answers from data to satisfy difficult and ill defined questions. It’s the mess of reality.
- Theoretical Machine Learning: This is about math and abstraction and idealized scenarios and limits and beauty and informing what is possible. It is a whole lot neater and cleaner and removed from the mess of reality.
Data Science Resources: Data Science Recipes and Applied Machine Learning Recipes
Introduction to Applied Machine Learning & Data Science for Beginners, Business Analysts, Students, Researchers and Freelancers with Python & R Codes @ Western Australian Center for Applied Machine Learning & Data Science (WACAMLDS) !!!
Latest end-to-end Learn by Coding Recipes in Project-Based Learning:
Applied Statistics with R for Beginners and Business Professionals
Data Science and Machine Learning Projects in Python: Tabular Data Analytics
Data Science and Machine Learning Projects in R: Tabular Data Analytics
Python Machine Learning & Data Science Recipes: Learn by Coding
R Machine Learning & Data Science Recipes: Learn by Coding
Comparing Different Machine Learning Algorithms in Python for Classification (FREE)
Disclaimer: The information and code presented within this recipe/tutorial is only for educational and coaching purposes for beginners and developers. Anyone can practice and apply the recipe/tutorial presented here, but the reader is taking full responsibility for his/her actions. The author (content curator) of this recipe (code / program) has made every effort to ensure the accuracy of the information was correct at time of publication. The author (content curator) does not assume and hereby disclaims any liability to any party for any loss, damage, or disruption caused by errors or omissions, whether such errors or omissions result from accident, negligence, or any other cause. The information presented here could also be found in public knowledge domains.
